% 定义变量
a = -5; % alpha0
h = 0.1; % 步长
x = 0; % 左端点
y = 2; % 右端点
num = (y-x)/h+1; % 端点数
t = linspace(x,y,num); % 时间变量
u = zeros(num,1); % 解变量
u(1) = 1; % u0
u(2) = (1+h*h)^2; % 附加u1
% 线性二步法
for i = 2 : (num-1)
u(i+1) = (1+a)*u(i)-a*u(i-1)+0.5*h*((3-a)*f_function(t(i),u(i))-(1+a)*f_function(t(i-1),u(i-1)));
end
% 输出
for i = 1 : num
fprintf("u(%f)=%.7f\n",t(i),u(i));
end
matlab 运行上述代码结果:
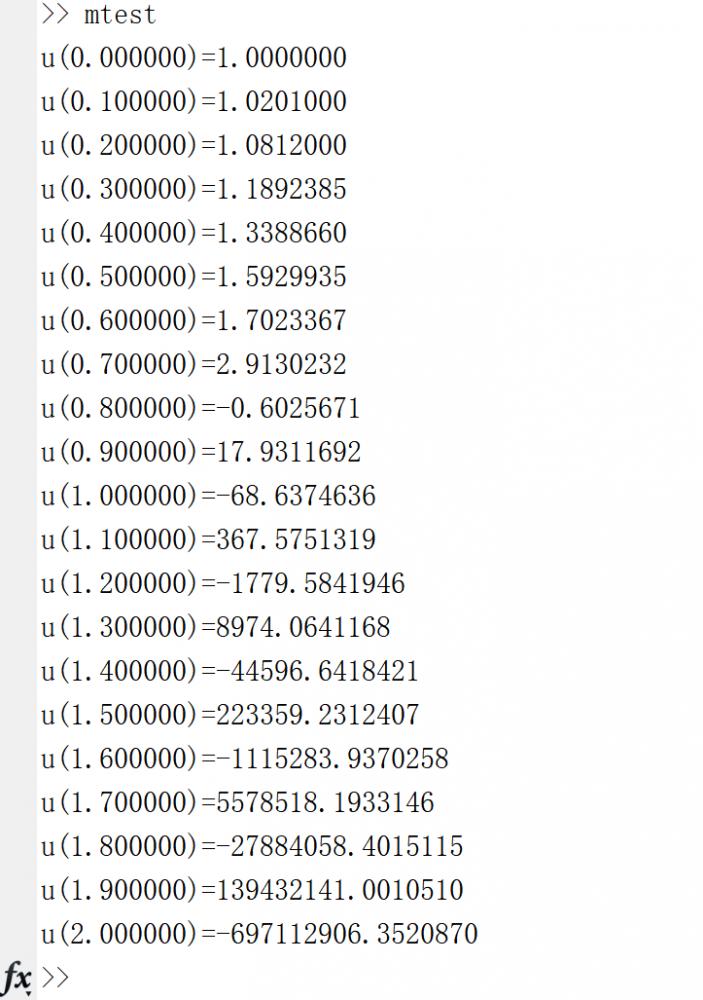
成人在线 软件运行上诉代码结果:

试了一下现在的北太4.2.1可以搞
% 定义变量
a = -5; % alpha0
h = 0.1; % 步长
x = 0; % 左端点
y = 2; % 右端点
% 定义 f_function 作为匿名函数
% 请根据你的具体微分方程修改下面的定义
f_function = @(t, u) u; % 示例: u' = u
% f_function = @(t, u) t + u; % 或者 u' = t + u
% f_function = @(t, u) t^2 + u^2; % 或者 u' = t^2 + u^2
num = (y-x)/h+1; % 端点数
t = linspace(x,y,num); % 时间变量
u = zeros(num,1); % 解变量
u(1) = 1; % u0
u(2) = (1+h*h)^2; % 附加u1
% 线性二步法
for i = 2 : (num-1)
u(i+1) = (1+a)*u(i)-a*u(i-1)+0.5*h*((3-a)*f_function(t(i),u(i))-(1+a)*f_function(t(i-1),u(i-1)));
end
% 输出
for i = 1 : num
fprintf("u(%f)=%.7f\n",t(i),u(i));
end
